Neural Parts: Learning Expressive 3D Shape Abstractions
with Invertible Neural Networks

Despoina Paschalidou 1,5,6 Angelos Katharopoulos 3,4 Andreas Geiger 1,2,5 Sanja Fidler 6,7,8
1 Autonomous Vision Group, MPI for Intelligent Systems Tübingen 2 University of Tübingen
3 Idiap Research Institute, Switzerland 4 École Polytechique Fédérale de Lausanne (EPFL)
5 Max Planck ETH Center for Learning Systems 6 NVIDIA 7 University of Toronto 8 Vector Institute
CVPR 2021

Paper
Code
Video
Poster
Slides
Blog

Our model learns to parse 3D objects into geometrically accurate and semantically consistent part arrangements without any part-level supervision. Our evaluations on ShapeNet objects, D-FAUST humans and FreiHAND hands demonstrate that our primitives can capture complex geometries and thus simultaneously achieve geometrically accurate as well as interpretable reconstructions using an order of magnitude fewer primitives than state-of-the-art shape abstraction methods.

Existing primitive-based methods rely on simple shapes for decomposing complex 3D shapes into parts. As a result, they require a large number of primitives for extracting accurate reconstructions. However, this results in less interpretable shape abstractions, namely primitives are not semantically meaningful parts.

Neural Parts is a novel 3D primitive representation that can represent arbitrarily complex genus-zero shapes and thus yield more geometrically accurate and semantically meaningful shape abstractions compared to simpler primitives.

Approach Overview

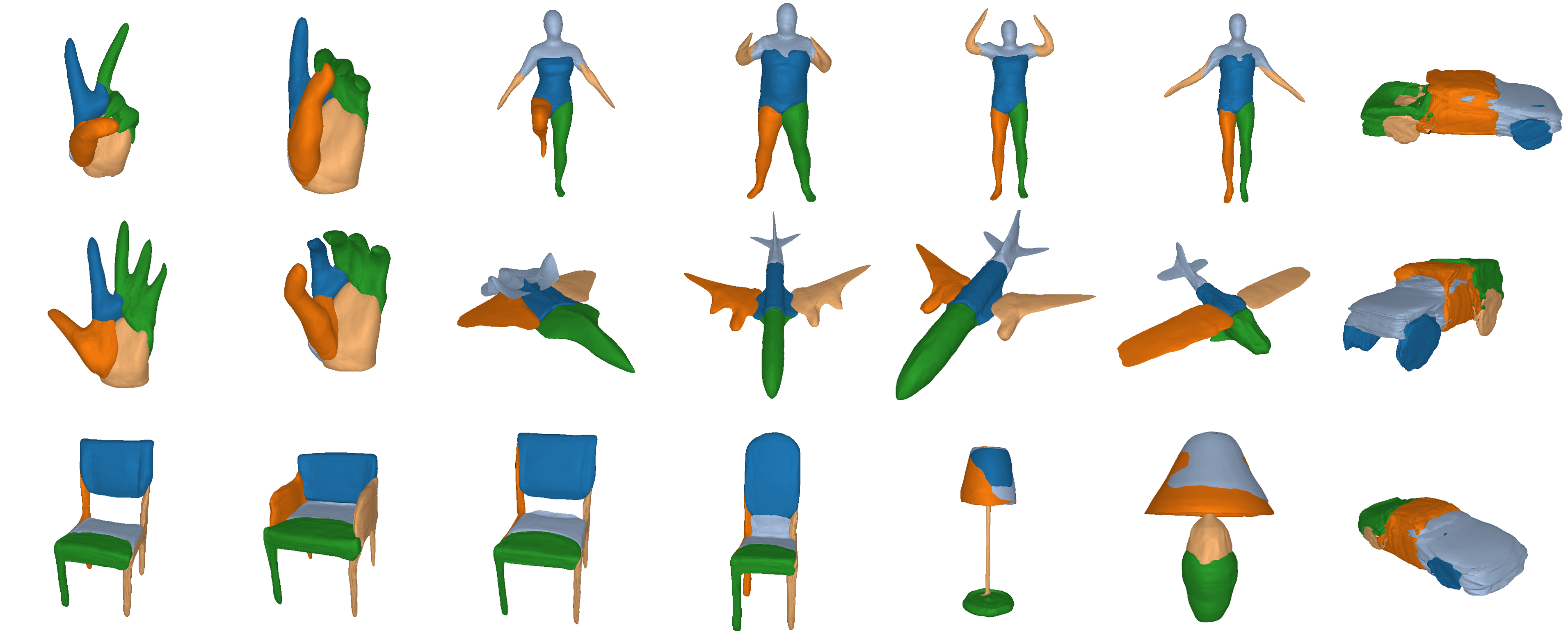
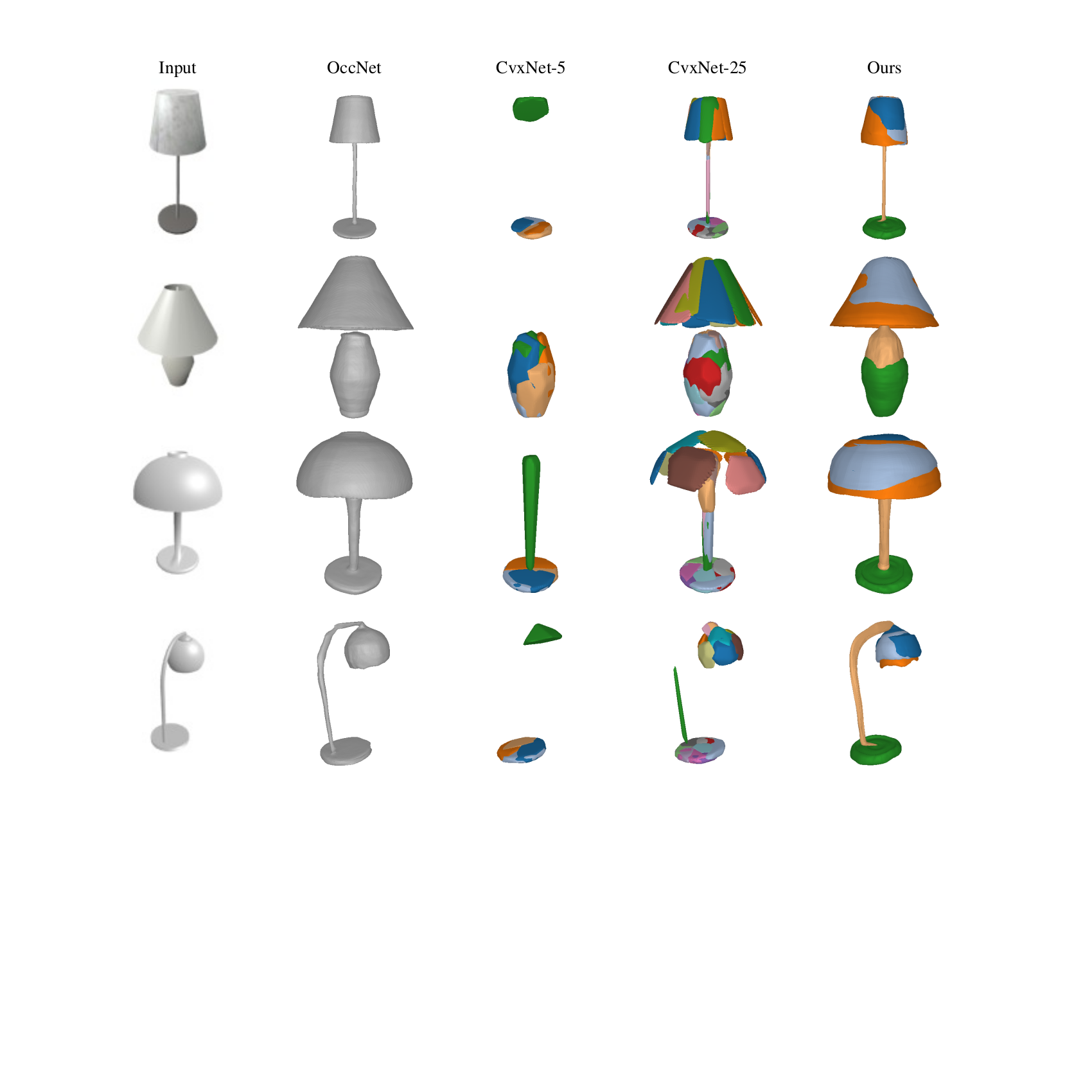
Primitive-based representations seek to infer semantically consistent part arrangements across different object instances. Existing primitive-based methods rely on simple shapes for decomposing complex objects into parts such as cuboids, superquadrics, spheres or convexes. Due to their simple parametrization, these primitives have limited expressivity and cannot capture arbitrarily complex geometries. Therefore, existing part-based methods require a large number of primitives for extracting geometrically accurate reconstructions. However, using more primitives comes at the expense of less interpretable reconstructions. Namely, a primitive is not an identifiable part anymore.

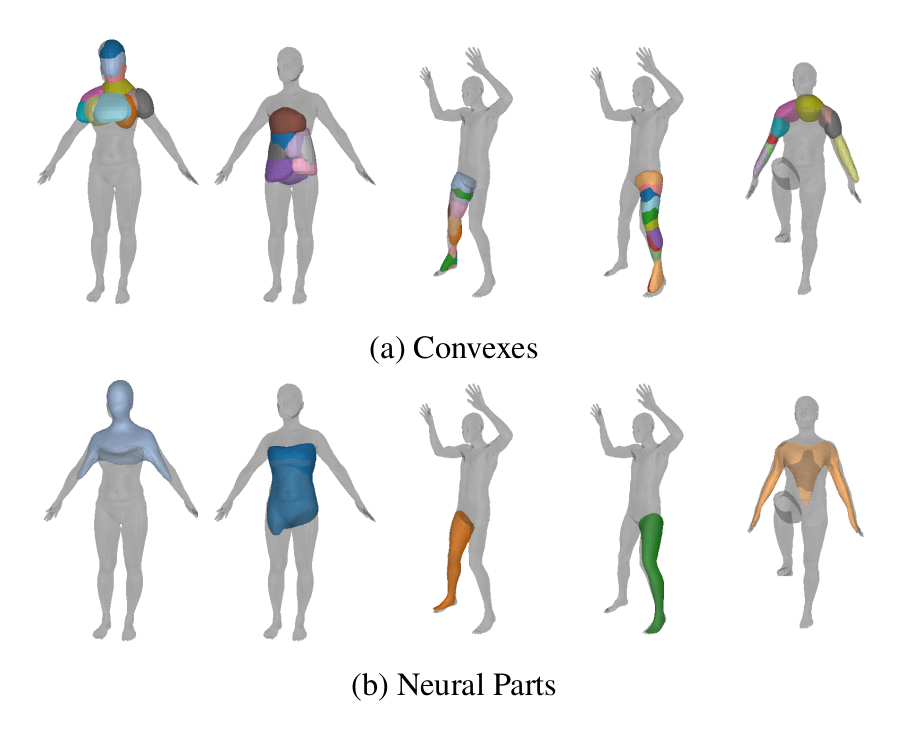
We introduce a novel 3D primitive representation that is defined as a deformation between shapes and is parametrized as a learned homeomorphic mapping implemented with an Invertible Neural Network (INN). We argue that a primitive should be a non trivial genus-zero shape with well defined implicit and explicit representations. Using an INN allows us to efficiently compute the implicit and explicit representation of the predicted shape and impose various constraints on the predicted parts. In contrast to prior work, that directly predict the primitive parameters (i.e. centroids and sizes for cuboids and superquadrics and hyperplanes for convexes), we employ the INN to fully define each primitive. This allows us to have primitives that capture arbitrarily complex geometries, hence the ability of our model to parse objects into expressive shape abstractions that are more geometrically accurate using an order of magnitude fewer primitives compared to approaches that rely on simple convex shape primitives.

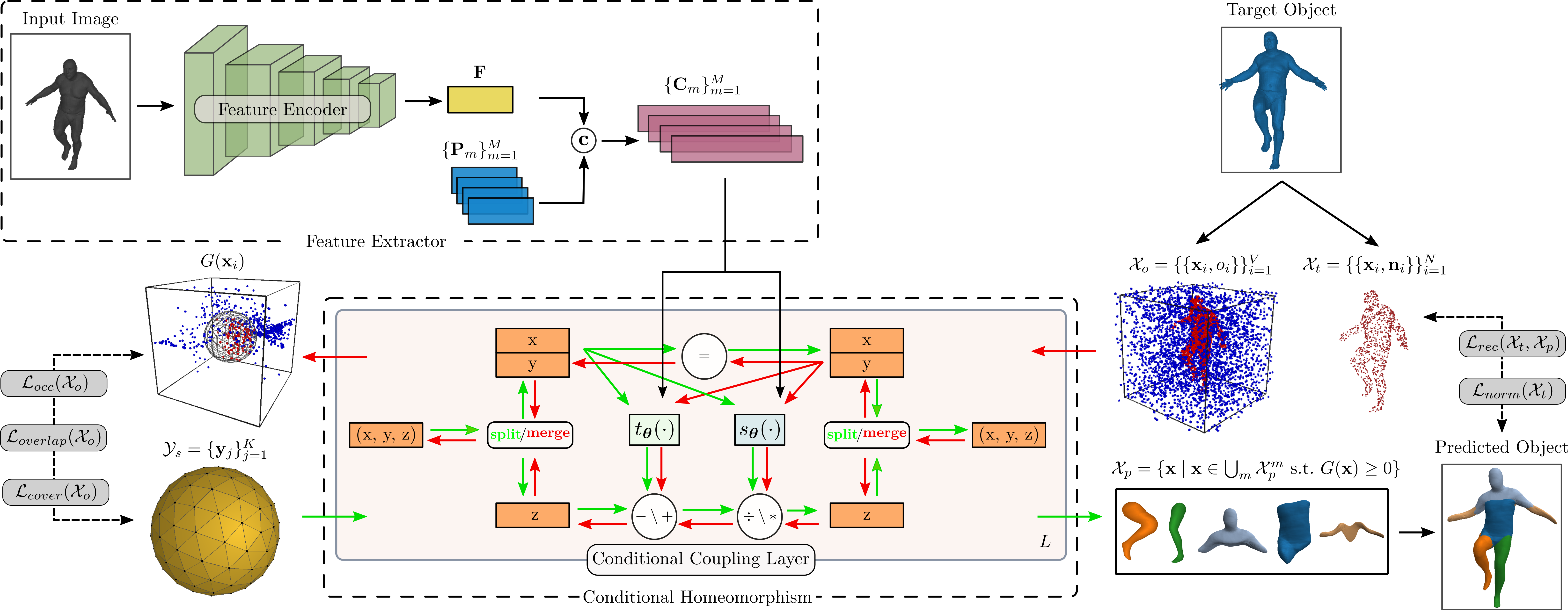
Given an input image and a watertight mesh of the target object we seek to learn a representation with M primitives that best describes the target object. We define our primitives via a deformation between shapes that is parametrized as a learned homeomorphism implemented with an Invertible Neural Network (INN). For each primitive, we seek to learn a homeomorphism between the 3D space of a simple genus-zero shape and the 3D space of the target object, such that the deformed shape matches a part of the target object. Due to its simple implicit surface definition and tesselation, we employ a sphere as our genus-zero shape. Note that using an INN allows us to efficiently compute the implicit and explicit representation of the predicted shape and impose various constraints on the predicted parts.

Results
In the following interactive visualization, the naming of the parts has been done manually. However, the model had no part supervision during training. The semantic parts have emerged naturally from reconstructing the geometry.

Humans

Show

Planes

Show
Comparison to Primitive-based Methods

We compare the representation power of Neural Parts to other primitive-based methods by evaluating the reconstruction quality with varying number of primitives on three datasets. We observe that our model is more geometrically accurate, more semantically consistent and yields more meaningful parts (i.e. primitives are identifiable parts such as thumbs, legs, wings, tires, etc.) compared to simpler primitives.

Semantic Consistency
We observe that Neural Parts consistently use the same primitive for representing the same object part regardless of the breadth of the part's motion. Notably, this temporal consistency is an emergent property of our method and not one that is enforced with any kind of loss.
Acknowledgements
This research was supported by the Max Planck ETH Center for Learning Systems.